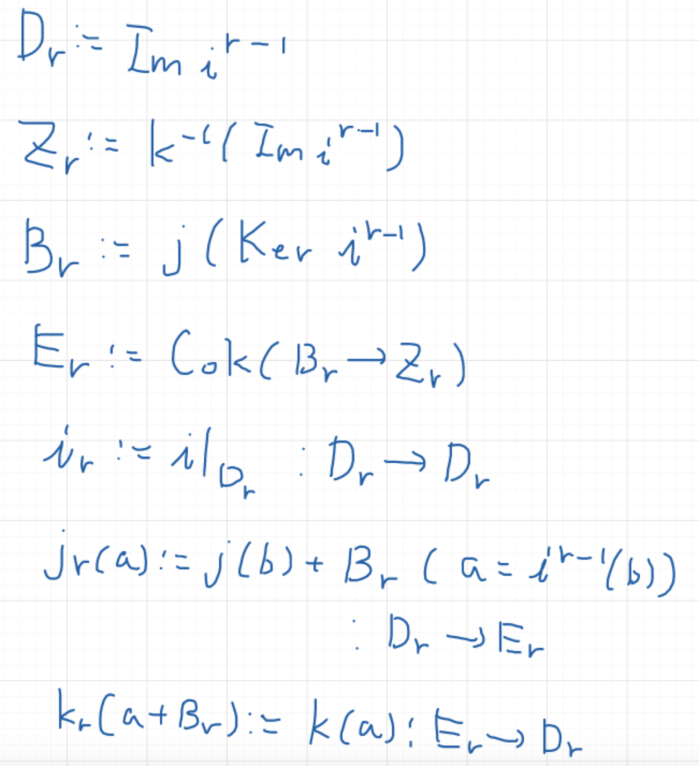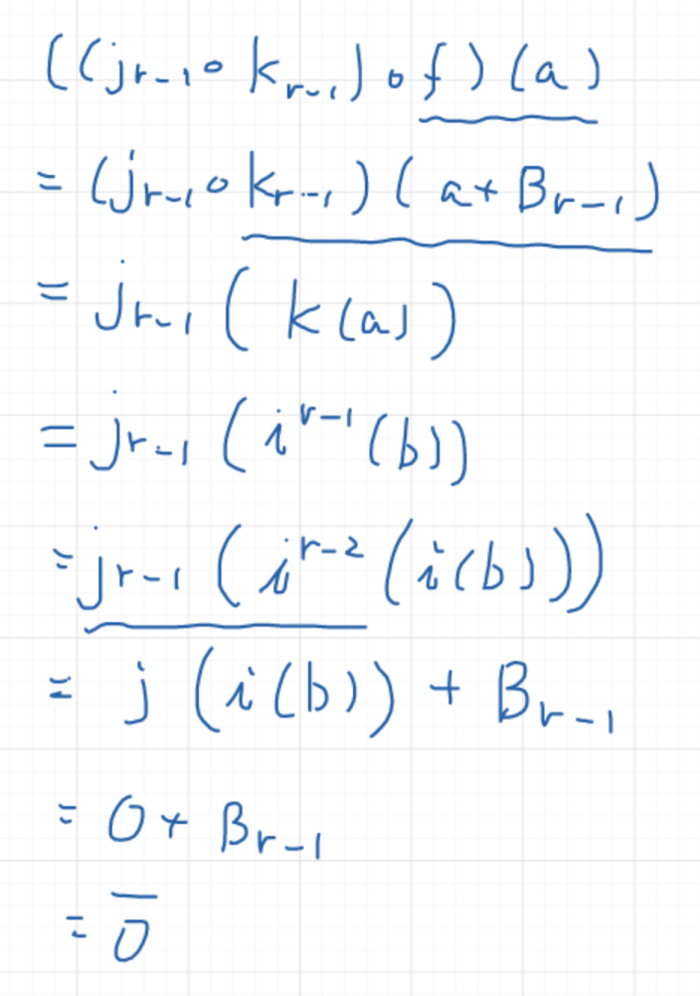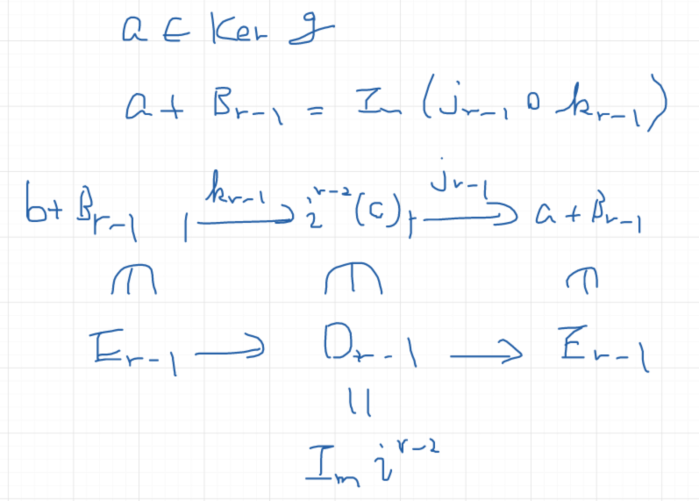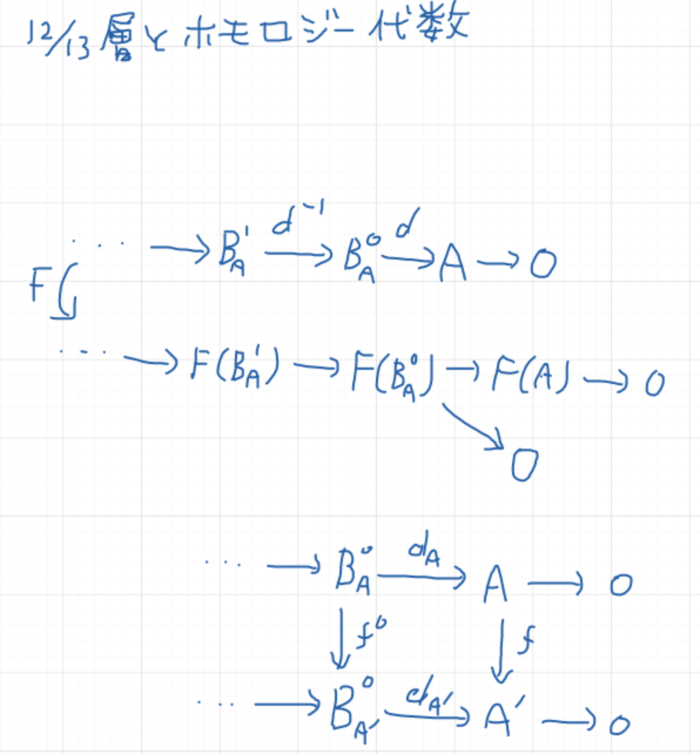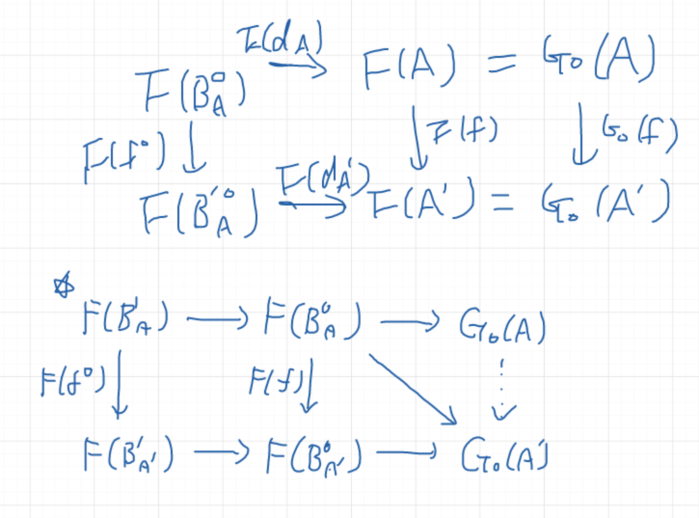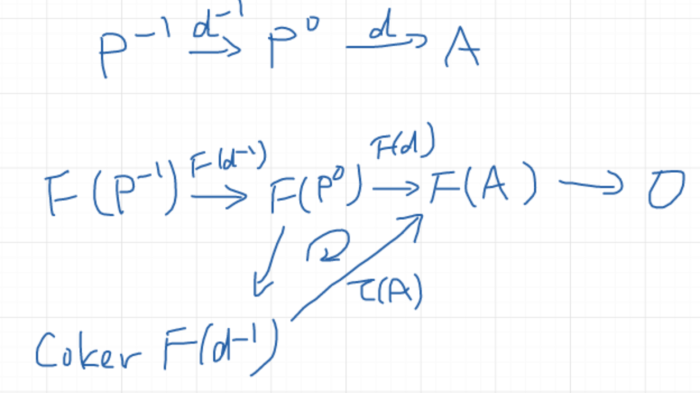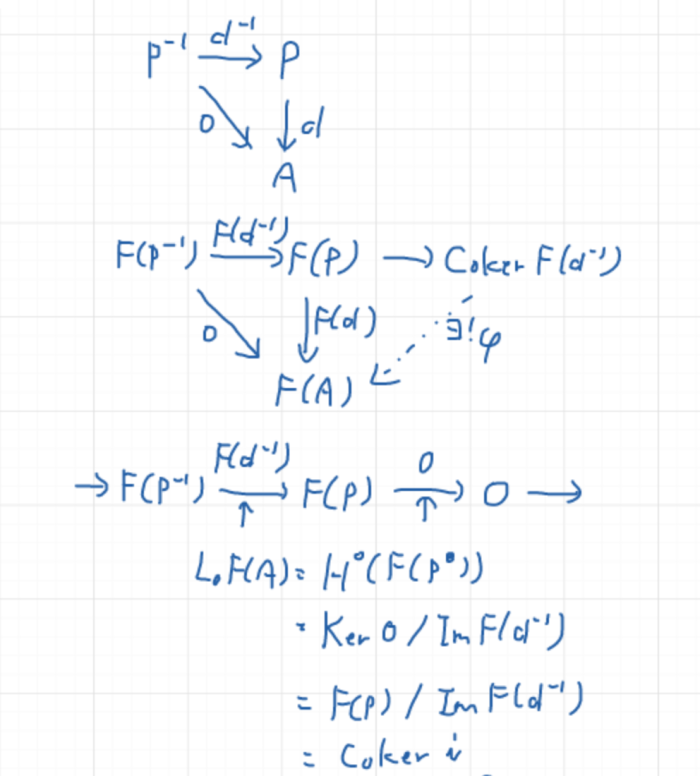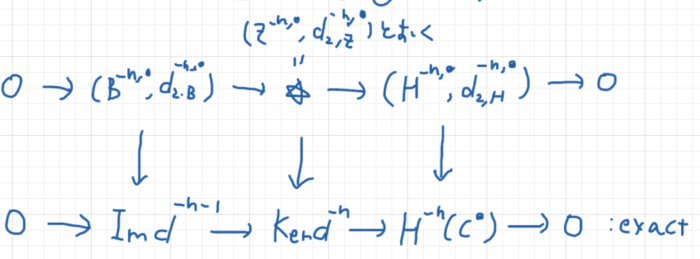【層とホモロジー代数】2018.5.30

○日時
2018.5.30 (水) 20:00〜22:00

○参加者
A, K

○発表者
A

○概要
第3章 ホモロジー代数 3.5 TorとExt 〜命題3.72の手前

○内容

• Torの定義
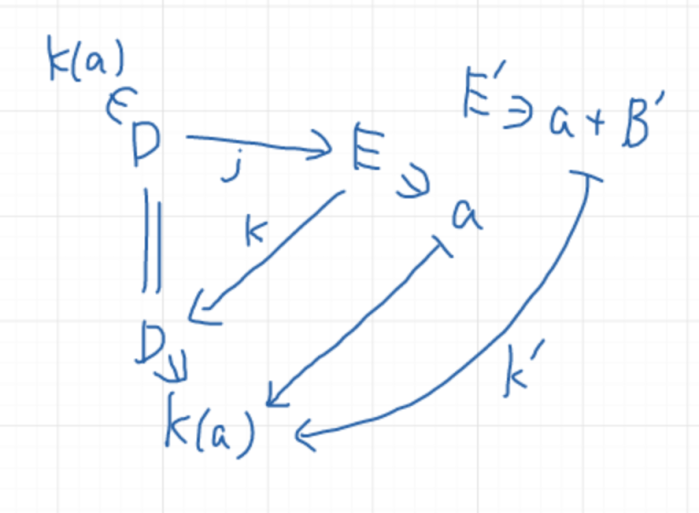
• Torの定義が射影的分解の取り方に依らないこと
• M |-> Tor^R_n(L, M), L |-> Tor^R_n(L, M) により Tor^R_n(-, M), Tor^R_n(L, -) が関手になること
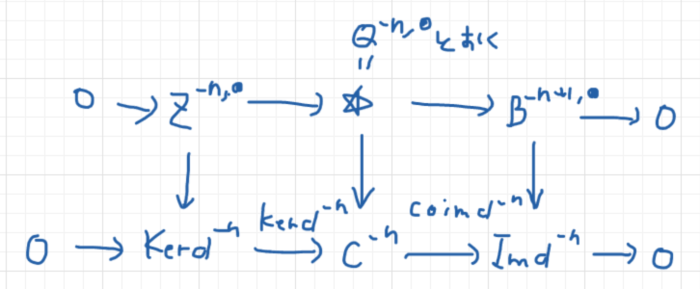
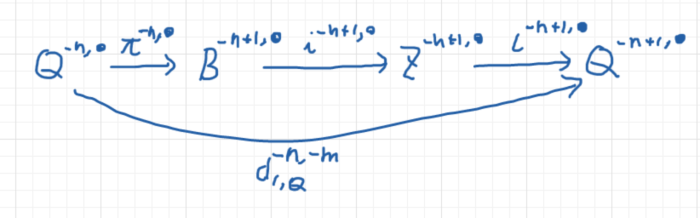
• これらの関手を使って、短完全列から長完全列への関手が定まること
• n=0のときのTorがテンソル積と一致すること
• これらの関手が帰納極限と可換であること

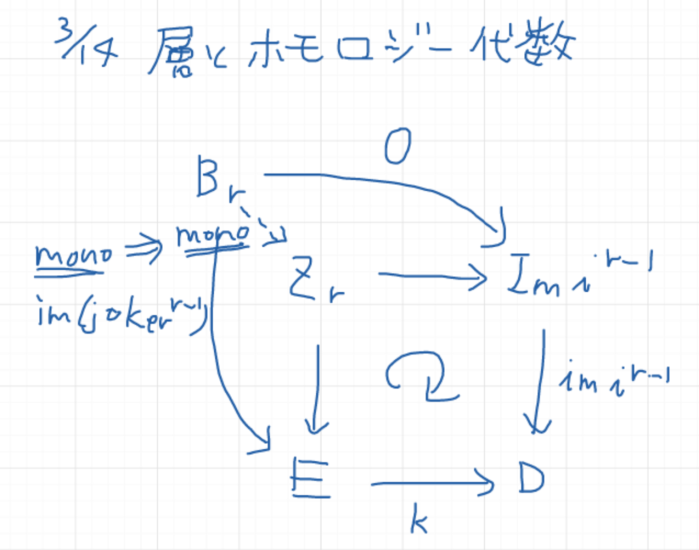
○板書

(無し)

○次回
2018.6.13

※テキスト
Jean-Pierre Serre, Local Fields, Springer

○今後

次回からMの参加が見込まれるため、新しいテキストに移る予定となった。

【層とホモロジー代数】2018.4.25

○日時
2018.4.25 (水) 20:00〜22:00

○参加者
A, K

○発表者
A

○概要
第3章 ホモロジー代数 3.4 スペクトル系列 系3.66〜3.4末尾

○内容

• アーベル圏における複体A^●と、ある条件を満たす二重複体K^{●,＊}の間を良い性質を持つ射が結んでいるとき、複体A^●のコホモロジーとK^{●,＊}の全複体のコホモロジーの間に自然な同型がある
• グロタンディーク-ルレイ スペクトル系列が存在すること

○板書

(無し)

○次回
2018.5.?
第3章 ホモロジー代数 3.5 TorとExt〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

○今後

このテキストの「3.6 群のホモロジーとコホモロジー」までは読むことにしようという意見でAとKが一致。他の人の意見が無ければこの方針で行く予定。

【層とホモロジー代数】2018.3.30

○日時
2018.3.30 (金) 20:00〜22:00

○参加者
A, K

○発表者
K, A

○概要
第3章 ホモロジー代数 3.4 スペクトル系列 注 3.58〜系 3.66の手前

○内容

• 二重次数付き完全対でも完全対と同じように導来対が定義できること
• 二重次数付き完全対でも第r導来対が定義でき、それが導来対を取る操作をr – 1回繰り返したものと一致すること
• 有界な二重次数付き完全対から自然にスペクトル系列が定まること
• アーベル圏Aにおけるフィルター付けされた複体(K^●, (F^p K^●))で、(F^p K^n)がK^nの有限なフィルター付けとなるとき、自然にスペクトル系列が構成されること
• M係数相対特異ホモロジーを例として、鎖複体からスペクトル系列が構成されるところまでの流れ

○板書

(無し)

○次回
2018.4.?
第3章 ホモロジー代数 3.4 スペクトル系列 注3.66〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

○今後

「そろそろ『層とホモロジー代数』にも区切りを付けて、新しい本を読む別の勉強会を始めるのでもいいのではないか」という提案が出て、A, Kともに同意。具体的な日程や読む本についてはまだ何も決まっていない。

【層とホモロジー代数】2018.3.14

○日時
2018.3.14 (水) 20:00〜22:00

○参加者
A, K

○発表者
A

○概要
第3章 ホモロジー代数 3.4 スペクトル系列 定義 3.55〜定義 3.57

○内容

• 第r導来対の定義
• 第r導来対の帰納的な定義と直接的な定義が一致すること
• 二重次数付き完全対の定義

○板書

○次回
2018.4.?
第3章 ホモロジー代数 3.4 スペクトル系列 注3.58〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

【層とホモロジー代数】2018.2.19

○日時
2018.2.19 (月) 20:00〜22:00

○参加者
A, K

○発表者
A, K

○概要
第3章 ホモロジー代数 3.4 スペクトル系列 定義 3.52〜定義 3.55

○内容

• 完全対 (exact couple) の定義
• 完全対から別の完全対 (導来対, derived couple) が生成できること
• 第r導来対の定義
• 完全対 (D, E, i, j, k) の E がスペクトル系列の E に相当するっぽい
• 完全対を抽象化して整理するとスペクトル系列につながっていくっぽい

○板書

○次回
2018.3.?
第3章 ホモロジー代数 3.4 スペクトル系列 定義3.55の次の段落〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

【層とホモロジー代数】2018.1.29

○日時
2018.1.29 (月) 20:00〜22:00

○参加者
A, K

○発表者
A, K

○概要
第3章 ホモロジー代数 3.3 導来関手 命題3.38〜 3.4 スペクトル系列 注3.51

○内容

• 3.3 導来関手
  • 非輪状対象の特徴付け、諸々の性質を満たすアーベル圏およびその対象の部分集合があったとき、全ての射影的対象がその集合に属し、集合の元が全て非輪状対象となっている。
  • （命題3.31〜注3.47までの定義、命題、注の双対）
• 3.4 スペクトル系列
  • フィルター付けの定義
  • アーベル圏におけるスペクトル系列の定義、『コホモロジーのこころ』とは別の流儀の定義を採用している。定義3.49の(5)がキモか (?)

○板書

○次回
2018.2.?
第3章 ホモロジー代数 3.4 スペクトル系列 定義3.52〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

【層とホモロジー代数】2017.12.13

○日時
2017.12.13 (水) 21:00〜22:00

○参加者
A, K

○発表者
K

○概要
第3章 ホモロジー代数 3.3 導来関手 命題3.37

○内容

• ある良い性質を持つアーベル圏では、F非輪状分解のホモロジーで定義される関手G_nから左導来関手L_n Fへの自然同値が存在する

○板書

○次回
2017.12.?
第3章 ホモロジー代数 3.3 導来関手 命題 3.38〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

【層とホモロジー代数】2017.11.15

○日時
2017.11.15 (水) 20:00〜22:00

○参加者
A, K

○発表者
A

○概要
第3章 ホモロジー代数 3.3 導来関手 命題3.33から命題3.36まで

○内容

• 右完全関手Fによる左導来関手LnFの特徴付け
• F非輪状対象とF非輪状分解の定義
• F非輪状分解から左導来関手が計算できること

○板書
(無し)

○次回
2017.12.?
第3章 ホモロジー代数 3.3 導来関手 命題 3.37〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

【層とホモロジー代数】2017.10.2

○日時
2017.10.2 (月) 20:00〜22:00

○参加者
A, K

○発表者
A

○概要
第3章 ホモロジー代数 3.3 導来関手 命題3.31から定義3.32まで

○内容

• アーベル圏の間の加法的関手F: A → Bに対して、射影的分解を使い導来関手LnF: A → Bが定義できること。
  • LnFの関手性
  • 導来関手の族(LnF)nが、関手SES(A) → ES(B)を定めること。
  • A ∈ Ob Aが射影的ならばLnF(A) = O (∀n ≧ 1)となること。
  • 自然変換τ: L0F → Fがあること。Fが右完全なら自然同値になること。
  • Fが完全ならLnF(A) = O (∀n ≧ 1, ∀A ∈ Ob A)となること。

○板書

○次回
2017.10.?
第3章 ホモロジー代数 3.3 導来関手 命題 3.33〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版

【層とホモロジー代数】2017.9.11

○日時
2017.9.11 (月) 20:00〜22:00

○参加者
A, K

○発表者
K

○概要
第3章 ホモロジー代数 3.2 射影的分解と単射的分解 命題3.22から注3.30 (3.2の終わり) まで

○内容

• 複体がよい性質を持つ二重複体に分解できること (左カルタン-アイレンバーグ分解)
  • アーベル圏の全ての対象の射影的分解が、ある添字より小さいところで消えている場合、先程の二重複体はあるところから左が消えていることになる。
• 定義3.24〜注3.30は定義3.17〜注3.23の双対。

○板書

○次回
2017.9.?
第3章 ホモロジー代数 3.3 導来関手〜

※テキスト
志甫淳, 層とホモロジー代数, 共立出版